Karin Englund

Knäckta julnötter

Postat den 7 januari, 2014 av Karin

Redaktörns julnötter var lite knäckande i år, tycker jag nog. Till och med ordkunskapsfrågorna – som jag betraktar som min bästa gren – var knepiga. Här är lösningarna.

I. Ordkunskap: homonymer

1.a Slakteriterm (KYL, benämning på lårben av lamm eller kalv)
1.b Finns i moderna kök (KYL)

2.a Tänk 80 (VAL. Räkneord. En kast var fyra strömmingar, 20 kast var en val, dvs 80)
2.b Tänk 1988, 1991 och 1994 ( VAL. Dessa år var riksdagsval)
2.c Tänk stort (VAL. Största däggdjuret)

3.a Viktigt för kockar (LAG. Behövs i marinader mm)
3.b Viktigt för fanatiker (LAG. Inte minst för Stockholms fotbollsfans)
3.c Viktigt för riksdagsledamöter (LAG. Riksdagens främsta uppgift är att stifta lag)

4.a Dröm för flicka ( BAL. Så underbart…säger Askungen)
4.b Dröm för kossa (BAL. Som i höbal)

5.a Mardröm för vattenvarelse (DRAG)
5.b Önskade bisarr greve (DRAG. Ian Wachmeister önskade ”drag under galoscherna”)

6.a Beundrad för sin styrka (RAM. Björnen är fruktad för sina starka ramar)
6.b Ofta mer värdefull än innehållet (RAM. På bondauktioner är ofta ramen mer värd än tavlan)

7.a Inget för den köpmedvetne (KRAM)
7.b Tillåtet för män på fotbollsplan (KRAM)

8.a Ingår i lekamen (VAD. En kroppsdel)
8.b Populärt i England (VAD. Spel om pengar)
8.c Förvillar spårhundar (VAD. Flyktingar som korsar vadställe kan lura förföljande hund)

9.a Gillar militärer (LED)
9.b Finns i fjällen (LED. Som i Kungsleden)
9.c Motoriskt oumbärlig (LED utan dem kan vi inte röra oss)

10.a Kan man räkna med (KAST= 4)
10.b Ingick i skolgymnastik (KAST med liten boll var en egen gren)
10.c Också en hierarki (KAST. Indisk klassindelning)
10.d Flugig förbindelselänk (KAST. Den tafs som förbinder flugspölina med fluga)
10.e För blytunga typer (KAST. Låda för förvar av blytyper)

På homonym nummer sex har en fyndig nötknäckare föreslagits ASK, som egentligen är en ännu bättre lösning. Träslaget ask är ju känt för sin styrka, används bland annat för att tillverka spjut. Och askar är ofta mycket mer värdefulla än det de innehåller.

II. Ren och skär logik – och konsten att avslöja lögner

1. En pojke och en flicka bekantar sig med varandra.
– Jag är en pojke, säger barnet med mörkt hår.
– Jag är en flicka, säger barnet med blont hår.
Åtminstone ett av barnen ljuger.

Fråga: Vilken färg på håret har pojken och vilken färg på håret har flickan?
RÄTT SVAR: Pojken har blont hår, flickan mörkt hår. Om man testar de olika alternativen – pojken ljuger/flickan ljuger/båda ljuger – ser man att gåtan bara kan lösas om båda barnen ljuger.

2. Du har framför dig tre tygpåsar om vilka du vet att var och en innehåller två ädelstenar. I en påse är båda ädelstenarna röda, i en påse är båda gröna och i en påse är en ädelsten röd och en ädelsten grön. Du vet att de röda ädelstenarna är 100 gånger mer värdefulla än de gröna. Du får ta två ädelstenar ur påsarna och behålla dem. Men hur ska du gå tillväga?

Du plockar först ur en slumpmässigt vald påse ut en ädelsten och den visar sig vara röd.

Ur vilken påse ska du nu plocka ut nästa ädelsten för att med största sannolikhet maximalt öka din rikedom? Eller spelar det ingen roll för din chans till maximal rikedom ur vilken påse du drar din nästa sten?

RÄTT SVAR: Sannolikheten till maximal rikedom är att du tar nästa ädelsten ur samma påse du dragit din första sten. Du har då 2/3 chans att få en röd ädelsten. Om du byter till en annan påse minskar din chans till 1/2.

Förklaring. Du vet att du inte kan ha dragit den första stenen från påsen med två gröna ädelstenar. Om du håller fast vid den påse du valde först finns tre möjligheter.

Du valde först påsen med två röda ädelstenar. Du drog sten röd nr 1. Kvarvarande är då röd nr 2.
Du valde först påse med två röda ädelstenar. Du drog sten röd nr 2. Kvarvarande är då röd nr 1.
Du valde först påsen med en grön och en röd sten.

Som synes kommer du två gånger av tre att maximera din vinst.

3. Statens finansinspektion har upptäckt en olaglig spekulation mot den svenska kronan. En undersökning visar att en av tre storbanksdirektörer måste vara skyldig. Av utredningen framgår att bara en av dem kan tala sanning, medan de två andra två måste ljuga konsekvent av olika skäl. På utredarens direkta fråga om vem som har svindlat den svenska staten får han följande svar:

Kalle Kulor: ”Jag är oskyldig”.
Girige Herbert: ”Jag är oskyldig”.
Förslagne Doris: ”Girige Herbert är den skyldige”.

”Tack för de svaren”, säger utredaren och ber sina polisassistenter arrestera en av de misstänkta direktörerna som skyldig till svindeln. Och du vet väl också vem som är skurken i detta drama?

RÄTT SVAR: Kalle Kulor är den skyldige.

Förklaring. Antag Girige Herbert är skyldig. I så fall talade både Kalle Kulor och Förslagne Doris sanning. Följaktligen var det inte Herbert. Antag istället att Förslagne Doris är skyldig. Isåfall talade både Kalle Kulor och Girige Herbert sanning. Följaktligen var det inte Doris. Antag slutligen att Kalle Kulor är skyldig. I så fall talade endast Girige Herbert sanning. Det stämmer med förutsättningarna ovan och alltså är Kalle den skyldige.

4. Du har just levt klart och befinner dig nu i Sankte Pers väntrum för att slussas vidare till antingen Paradiset eller Helvetet. Men Paradiset håller på att bli överbefolkat så Sankte Per har föranstaltat en liten test för applikanterna.

I väntrummet som du förts in i finns bara två utgångar varav den ena leder till Paradiset och den andra till Helvetet. Men du vet inte vilken utgång som leder vart. Varje utgång vaktas av en dörrvakt varav den ena konsekvent ljuger och den andra konsekvent talar sanning. Men du vet inte vilken. Du har därmed ingen aning om det är lögnaren som vaktar dörren till Paradiset eller om det är sannıngssägaren.

Sankte Per säger att du får bara ställa en enda fråga som kan besvaras med enbart ja eller nej till en av dörrvakterna för att ta reda på dörren till Paradiset. Han påpekar att de båda dörrvakterna är införstådda med valsituationens villkor. Du svarar gnälligt att uppgiften är omöjlig att lösa eftersom du varken vet vilken av dörrvakterna som ljuger eller vart dörrarna går. Sankte Per skrattar gott och säger att en enda fråga räcker, men vem har sagt att det ska vara lätt att komma till Paradiset. Och om du tänker efter noga kommer du nog på den enda möjliga frågan.

RÄTT SVAR. Du måste ställa en fråga som involverar båda vakterna. Så här till exempel: ”Vad svarar din kollega om jag frågar honom om din dörr leder till Helvetet?” Det finns fyra möjliga kombinationer av dörrar och vakter.:

Vakten du vänt dig till är sanningssägare och vaktar dörren till Helvetet. Hans svar på frågan blir NEJ (eftersom han vet att kollegan som ljuger skulle svara detta)
Vakten du vänt dig är lögnare och vaktar dörren till Helvetet. Han svar på frågan blir NEJ (eftersom han vet att den andre vakten som talar sanning skulle sagt ja)
Vakten du vänt dig till är sanningssägare och vaktar dörren till Paradiset. Hans svar på frågan blir JA (eftersom han vet att lögnaren skulle svarat ja)
Vakten du vänt dig till är lögnare och vaktar dörren till Paradiset. Hans svar på frågan blir JA (eftersom han vet att sanningssägaren skulle ha svarat nej).

Av dessa möjliga svar kan du dra slutsatsen att vid ett JA-svar står du framför dörren till Paradiset. Vid ett NEJ-svar står du framför dörren till Helvetet. Du behöver följaktligen inte känna till om du vänt dig till sanningssägaren eller lögnaren för att lista ut vilken dörr du ska välja. (Logiken i denna lösning är att dubbla negationer tar ut varandra, ungefär som vi matematiken fick lära -1 x -1 = +1)

Följande samtal äger rum:

Karin: ”Jag vet inte vilka siffrorna är.”
Gunnar: ”Inte jag heller, men jag visste att du inte kunde veta det.”
Karin: ”Vad bra, nu vet jag vilka de två siffrorna är!”
Gunnar: ”Jag med!”

Vilka är de två siffrorna?

RÄTT SVAR. A = 2 och B = 2.

Det här är en av de svåraste gåtor jag känner till. Men faktum är att varje yttrande av Karin och Gunnar ger oss lite extra information så att vi logiskt kan räkna ut lösningen. Så här ska man resonera.

(i) ”Jag vet inte vilka siffrorna är”.

Det här säger oss att Karins summa inte kan vara 0, 1, 17 eller 18. (Om den vore det skulle nämligen Karin känna till båda siffrorna. Summan 0 är ju lika med 0+0, summan 1 är lika med 0+1, summan 17 lika med 8+9 och summan 18 lika med 9+9).

(ii) ”Inte jag heller, men jag visste att du inte kunde veta det”

Detta ger oss mer information. Gunnar kan bara ha någon av produkterna 4, 6, 8, 9, 12, 16, 18, 24 och 36. Om Gunnar haft någon annan tänkbar produkt skulle han redan ha vetat siffrorna (exempelvis kan produkten 5 bara uppstå med multiplikationen 1 x 5, produkten 7 med 1 x 7, osv. Testa vidare själv). Observera att Gunnar inte kan ha produkten 0 (som ju uppstår när 0 multipliceras med vilken siffra som helst). Om han haft det skulle han nämligen inte kunnat påstå att han visste att Karin inte kunde känna till siffrorna. Gunnar kan ju i detta fall inte utesluta att Karin haft summan 0, vilket skulle inneburit att hon hade känt till siffrorna från början, se (i) ovan.

(iii) ”Vad bra, nu vet jag vilka de två siffrorna är”

Karins vetskap ger oss viktig information. Hon upplyser ju oss om att av hennes tänkbara siffror finns bara en kombination som ger någon av produkterna i (ii) ovan. En genomgång av summorna visar dessa måste vara 4, 12 eller 13 vilka entydigt pekar på produkterna 4, 36 och 36. (Om till exempel summan varit 5 kan ju Karin inte veta om produkten var 4 (1×4) eller 6 (2×3). Samma mångtydighet gäller alla andra summor utom 4, 12 eller 13.)

Vi kan därför dra slutsatsen att Karin måste ha endera av sifferkombinationerna (2,2), (6,6) eller (4,9). (Varje kombination svarar mot en bestämd summa och det är därför Karin redan nu vet svaret. Observera att Karin vet att summan fyra inte kan uppstått genom 1+3, ty de siffrorna ger produkten 1 x 3 = 3, och om så vore fallet skulle Gunnar redan känt ha till siffrorna vilket han ju inte gör).

(iiii) ”Jag med!”

Gunnar kan enligt (iii) bara ha produkten 4 eller produkten 36. Men om han haft produkten 36 kunde han inte varit säker på vilka siffrorna varit; de kunde ju uppstå genom multiplikationen 6 x 6 eller genom multiplikationen 4 x 9. Men eftersom Gunnar nu är säker på svaret måste han ha produkten 4. Denna produkt kan bara ha uppstått genom multiplikationen 2 x 2, eftersom multiplikationen 1 x 4 inte är möjlig för då skulle Karin haft summan 5 och enligt (iii) ovan inte kunnat ha känt till lösningen.

Gunnar kan alltså nu veta att rätt svar är A=B=2. Och det kan du också veta om du förstått hur Gunnar kommit fram till denna slutsats.

III. Optiska villor, andra villor och lite fysik

Varje julnötstävling bör innehålla ett tändsticksproblem. I uppställningen nedan är uppgiften att flytta en enda sticka så du får en korrekt ekvation (åtminstone om du nöjer dig med två decimaler).

Vilken sticka vill du flytta och varthän?

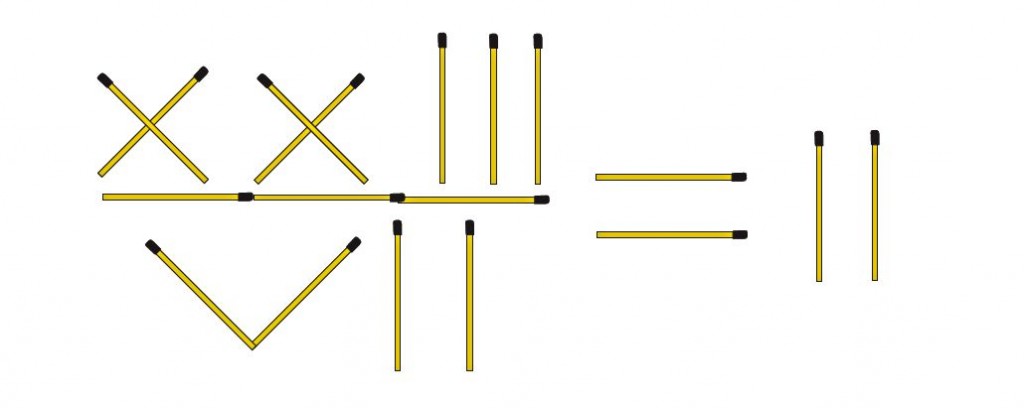RÄTT SVAR. Du flyttar den högra stickan i talet XXIII till andra sidan likhetstecknet och lägger stickan vågrätt över II på så sätt att symbolen för talet pi bildas. Ekvationen blir då 22/7 = pi.

Med två decimaler är 22/7 lika med 3,14 vilket också är pi skrivit med två decimaler.

2. Två pojkar vill ta sig över en å. Båda pojkarna är dåliga simmare och skulle drunkna om de försökte ta sig simmande över ån. Enda sättet att ta sig över är därför att använda en liten båt, som bara kan ta en person åt gången. Båten kan inte återvända på egen hand och den dras inte med rep eller andra anordningar, ändå lyckas de båda pojkarna ta sig över ån. Hur förklarar du det?

RÄTT SVAR. Pojkarna befann sig på var sin sida av ån.

3. En gurka består till 99% av vatten. Efter att ha legat i solen på ett bord ett längre tag består den bara till 98% av vatten. Hur mycket väger gurkan nu om den från början vägde ett kilo?

RÄTT SVAR. Gurkan väger 1/2 kg eller 500 gram.

Intuitivt känns svaret överraskande. När gurkan till 99% bestod av vatten var den fasta massan 10 gram. När gurkan består av 98 procent vatten ska de fasta massan om 10 gram följaktligen utgöra 2 procent av gurkans vikt. Om vi antar att den skrumpna gurkans vikt är X kan vi ställa upp följande ekvation 2/100 x X = 10 vilket ger X = 100 x 10/2 vilket ger X = 500.

4. Erik kör sin motorcykel ett varv (= 1 km) på en motorbana i 30 km/t. Han ska köra ett varv till och vill efter det varvet ha kört de båda varven med en medelhastighet av 60 km/t. Hur fort måste han köra det andra varvet för att teoretiskt klara av uppgiften? (OBS. Svaret är INTE 90 km/t).

RÄTT SVAR. Detta betyder ju att Erik vill köra två varv på exakt samma tid som det första, dvs att han ”teoretiskt” måste köra det andra varvet på ingen tid alls, dvs med oändligt hög hastighet. Eftersom enligt Einstein inget kan färdas fortare än ljuset är detta ännu så länge omöjligt.

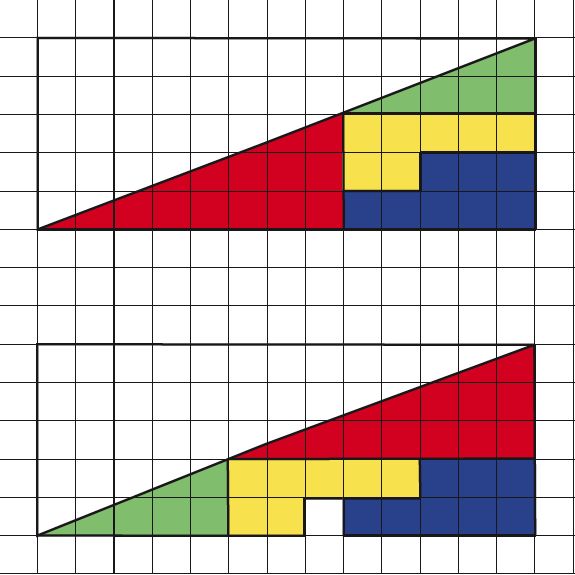
5. Betrakta de två trianglarna nedan. De är byggda av samma färgglada bitar, men i den nedre triangeln har smugit sig in en vit kvadrat. Kan du förklara hur den har uppstått?

___________________________________________________________________________________

RÄTT SVAR. Hypotenusan i de båda trianglarna är inte riktigt rät. I den övre triangeln buktar hypotenusan lätt inåt och i den nedre buktar den lätt utåt. Den lilla skillnaden ger det utrymme som behövs för att skapa den vit fyrkanten i den nedre triangeln. (Om man skriver ut figuren på papper och tittar på utskriften snett från sidan går att se att linjerna buktar).

Årets vinnare, som får ett exemplar av Det tänkande hjärtat av Yvonne Hirdman, är familjen Ehlin-Kolk som lyckades knäcka 18 av 20 nötter, med hjälp av grupparbete som också involverade andra än den omedelbara familjen. Kudos!

Publicerat i Tävling | Etiketter julnötter, lösning | 11 kommentarer

Julens tolv dagar

Postat den 6 januari, 2014 av Karin

Trettondedag? Hur då? Undrar någon och jag plockar fram mina gamla skolkunskaper, väl medveten om att de nog kan ha blivit omsprungna av senare forskning.

– Jo, Jesus föddes ju den 25 december…

– Va? Han föddes väl på julafton?

– Nej, det är dagen innan själva dagen, det är därför det heter afton. Han föddes den 25 december. Och då syntes en stjärna och några herdar som var ute och vallade får fick syn på den och gick åt det hållet och så hittade de Jesus i stallet på trettondagen.

– Herdar? Var det inte kungar? Guld och rökelse och allt det där.

– Jo visst ja! Först kom herdarna som hört av några änglar i Betlehemstrakten att Jesus var född. De kom nog redan på annandagen. Och sedan, på trettondagen, kom kungarna, eller de vise männen, eller stjärntydarna som det står i numera i nya testamentet.

Här kommer de med sina gåvor, Baltassar, Melchior och Caspar på en mosaik i Ravenna från 500-talet

Bäst att kolla källan, tänker jag och letar fram Matteusevengeliet. Oj, det var visst mer dramatiskt än jag mindes. Kung Herodes hade hört talas om att det var något på gång och ville veta om det verkligen var så ett en ny härskare hade fötts. Så det var han som kallade på stjärntydarna: ”’Bege er dit och ta noga reda på allt om barnet’, sade han, ’och underrätta mig när ni har hittat honom, så att också jag kan komma dit och hylla honom.’ Efter att ha lyssnat till kungen gav de sig i väg, och stjärnan som de hade sett gå upp gick före dem, tills den slutligen stannade över den plats där barnet var. När de såg stjärnan fylldes de av stor glädje. De gick in i huset, och där fann de barnet och Maria, hans mor, och föll ner och hyllade honom. De öppnade sina kistor och räckte fram gåvor: guld och rökelse och myrra. I en dröm blev de sedan tillsagda att inte återvända till Herodes, och de tog en annan väg hem till sitt land.”

Här är en mosaik från omkring år 300, med Jesus som den återfödda – eller obesegrade – solen. Den finns i Vatikanens grottor i Rom.

Nyligen hörde jag dock i ett radioprogram att Jesus troligen föddes på sommaren. Men av taktiska skäl har hans födelsedag förlagts till vintern.

I romarriket firades solgudens pånytt-födelse den 25 december. Så när den romerske kejsaren Konstantin införde kristendom i sitt rike på 300-talet såg han också till att kristna solhögtiden.

Sedan hakade påven Liberius på, år 354 och beslöt att Jesu födelse inföll den 25 december. Och så har det förblivit i den västkristna kyrkan. Inom östkyrkorna är det oftast just den 6 januari som betraktas som Jesu födelsedag.

Och så var det det där med julens tolv dagar, som det heter i England. Eller i Tyskland. Där räknar man från den 26 och då blir det ju tolv dagar. Medan vi envisas med att julafton är viktigast och så räknar vi från juldagen och då blir det trettondedagen idag.

En populär engelsk sång handlar om julens tolv dagar. Det börjar med en rapphöna i ett päronträd och så läggs det till något varje dag, för att sluta med tolv trumslagare. Här är en bit av Nick Parks version, som SVT visade i julas. Tillgänglig till den 19 januari.

PS: På bloggen På livets trassliga bastmatta finns lästips för alla julens tolv dagar. Värt att botanisera bland!

PPS: De som har klurat på redaktörns julnötter börjar kanske undra var den utlovade lösningen är. Lugn, den är på väg. Vi måste bara kolla att nötterna inte hunnit bli mögliga, eller nåt. Lösningen kommer inom kort på denna blogg!

Publicerat i Att tolka, historia, konst | Etiketter Julens tolv dagar, stjärntydare, tre vise män, trettondedag | 4 kommentarer

Nytt år – ny partner?

Postat den 3 januari, 2014 av Karin

HeLenas passande förslag till lördagstema medan året är alldeles färskt är: Nytt år.

Mina förväntningar inför det nya året sammanfattas bäst med att jag tycker det är bra som det är. Jag önskar mig inga större förändringar, annat än möjliga hälsoförbättringar för dem som behöver det. Men någon ny partner vill jag inte ha och det vill inte redaktörn heller.

när man är två

Hör ni det, ni som skickar sådana här kort till honom med förslag om en liten träff där han kan få registrera sig alldeles gratis och få sig en snygg profil inlagd i en databas med oräkneliga damer som gärna träffar just en sådan som han. Grrrr… säger jag och känner hörntänderna växa. Var kommer de över sådana adresser undrar jag. Är det skatte-myndigheten (som svarar för folkbokföringen) som bättrar på kassan med att sälja adresslistor över ogifta män?

Av texten på kortet förstår man dels att det är svårartad karlbrist i branschen och dels att de inser att deras adressregister har sina brister. ”Skulle du råkat ha träffat någon nyligen och därför inte är intresserad av att bli hoptussad med en partner kan du bortse från detta meddelande.” Står det väl inte ordagrant, men på ett ungefär.

Hallå, vi är visserligen inte gifta men vi har sammanbott i ordnade former i decennier! Redaktör’n tar dock det hela med ro och konstaterar att det nog ändå är bättre med bristfälliga register än alltför korrekta och detaljerade.

Här finns övriga lördagsbloggare: Gnuttan Helena Karin på Pettas Livsrummet musikanta Olgakatt, Pysseliten

Publicerat i Livet | Etiketter dåligt förslag, dejtingsajt, Nytt år | 16 kommentarer

Flytta myror

Postat den 1 januari, 2014 av Karin

Från köksbordet har man numera utsikt över en mycket stor myrstack (eftersom vi har huggit ner en dunge gamla björkar). Myrorna har i stort sett drivit bort oss från halva tomten de senaste åren. I skydd av den timrade överbyggnaden till en stor jordkällare på granntomten har de byggt något som kan vara kommunens största myrstack.

När vi åt frukost i går, syrran och jag med myrstacken i blickfånget, tog vårt beslut form: Vi flyttar den! Så det gjorde vi och det blev ett väldigt trevligt workoutpass. Myrstacken fanns inte bara på utsidan utan också inuti byggnaden.

Och idag gjorde sig nyupptäckta myrstacksflyttarmuskler till känna på lite oväntade ställen.

Nu har myrorna flyttat. Utom möjligen de som bor under bodgolvet, men dem får vi ta ett snack med i vår när solen tittar fram.

Ja se det var en riktig nyårsworkout!

PS. Jag är dålig på att ta bilder innan jag sätter igång. När man sedan står där med ett nyrenoverat rum, en rensad rabatt, eller en flyttad myrstack, inser man att man borde tagit bilder på hur det såg ut innan. Syrran är bättre på det och det är hon som fotat flytten.

Publicerat i Livet | Etiketter Myrflytt, nyårsaktiviteter, workout | 20 kommentarer

Mot ljusare tider

Postat den 31 december, 2013 av Karin

Det är kanske så här björnarna ska tas? Det finns björn i våra trakter och jag gillar’t inte.

Jag var ute och cyklade på småvägar i Grönsinkatrakten när jag hörde en gren som knakade och tänkte att med ett så pass kraftigt knak måste det vara en älg. Så jag spanade in bland buskar och trädstammar och såg en lurvig rygg. Lustig älg som går på knä, tänkte jag. Men så insåg jag att det måste vara en björn och medan den lufsade bort från mig så fort den kunde vände jag om och cyklade hem så fort jag kunde. Vettskrämd.

Men när vi diskuterade björnar idag, redaktörn, syrran och pensionären och jag, så får jag höra att min björnrädsla är obefogad. Björnar angriper bara folk som är ute i skogen med jakthund och bössa. Skulle de mot all förmodan intressera sig för en fridsam bärplockare är det bara att stå alldeles still så tappar den intresset för en. Bara!

Men det var ju inte det jag skulle säga, utan tack för i år, var försiktiga i trafiken, akta er för nyårssmällare och allting annat farligt. Tänd ett tomtebloss i stället… Måtte 2014 blir ett trevligt, roligt, kreativt, omväxlande och fridsamt år!

Publicerat i Livet | 12 kommentarer

Inbrott, utbrott, avbrott

Postat den 30 december, 2013 av Karin

När man inte tittat till sina stugor på ett tag nalkas man dem med viss bävan. Sex veckor sedan vi var här senast och mycket kan hinna hända. I skogen bakom huset ligger träden som plockepinn efter stormarna och vi inser att det var i sista minuten som vi lät hugga ner de urgamla ruttna björkarna intill huset.

plockepinn

Just i slutet av november och början av december brukar mössen tröttna på utomhusliv och ta sig in i husen, så nästa kontroll handlar om vad de kan ha ställt till med. Denna milda höst verkar dock musinbrotten mest vara små artighetsvisiter. Inga elledningar är avgnagda och jag hittar inget musbo i tvättkorgen. Men tulpanlökarna, som jag inte hann sätta i höstas, är uppätna.

inbrott

Och musfällan som jag glömde att gömma (den är till för att fånga levande möss som sen släpps ut i skogen) har de tagit sig in i, ätit upp brödbiten och sedan brutit sig ut! Det är begåvade möss i de här trakterna. Min farbror brukade skryta om sina fenomenalt skickliga möss och de nya musgenerationerna verkar inte vansläktas.

För att släppa ut den mus som hamnat i fällans stängda del, måste en annan mus hoppa upp på taket och dra upp den där lilla spärren som håller fast plåtluckan. Och det verkar vara precis vad som hänt.

Sedan tog de några tuggor av stålullen innan de tröttnade på detta påvra hus och drog vidare. Det varma vädret har många fördelar: lägre elräkningar, lättkörda vägar, ingen snöskottning och färre möss i husen.

På minussidan är det väl främst det dåliga skidföret som man kan klaga på, men fördelarna överväger, tycker jag nog. Och vinterlandskapet kan vara vackert ändå.

decembersjö

Och avbrottet då? Jo, när klockradion står och blinkar vet man att det varit elavbrott. Men eftersom det inte varit kallt någon längre period är det inga vattenledningar som frusit sönder. Vi stoppar om husen så gott vi kan för att de ska klara nästa år också.

Publicerat i Livet | Etiketter möss, snöfritt, Storm | 6 kommentarer

En förbryllande film, Gloria

Postat den 29 december, 2013 av Karin

Den finns på tidningarnas listor över bästa filmer just nu. Den vann pris för bästa kvinnliga skådespelare vid Filmestivalen i Berlin i år. Gloria verkar vara filmen som ingen vågar kritisera. Jag såg den på annandagen och får ingen rätsida på den. Funderar lite på vad som irriterar mig bortsett från att man valt en osannolikt o-charmig manlig huvudperson. Paulina Garcia är verkligen makalöst bra i rollen som Gloria, hon förtjänar de priser hon får, men filmen är konstig, hennes rollkaraktär är konstig.

”Delvis dialogdriven” sade någon recensent. Onödigt prat, tycker jag. ”Levnadsglad” säger bioreklamen. Sorglig och trasslig, tycker jag. Inte kan det väl vara så enkelt att alla är helt till sig för att vi får se en vuxen kvinna som raggar på krogen och som gillar sex?

Hon känns lite för ogenomtänkt. De olika episoderna ger henne ingen personlighet, de är som plockade lite här och där och hon (Garcia) gör det bästa av dem, men Gloria blir alltmer ogripbar. Om någon skulle sabba min mobil, genom att släppa ner den i soppan och sedan skratta ut mig skulle jag nog bli rätt förbannad. I filmen framställs det som helt OK, rentav bra att Gloria gör det.

Gloria och ex-maken har trevligt tillsammans…

När Gloria tar med sin nyfunna partner, Rodolfo, till sin sons födelsedagsfest hamnar Rodolfo helt utanför medan hon blir sentimental med sin exmake, över deras gemensamma bröllopsbilder. Rodolfo blir sur och går. Undrar om inte jag hade gjort likadant.

Sympatierna hamnar liksom ingenstans i denna vaga historia. Kanske det är poängen? Men manuset saknar riktning och de medverkande tycks ha tappat intresset när de kommit halvvägs. ”Meh, måste filmen hålla på en halvtimme till? Vad ska vi hitta på då?”

Finns det dimensioner som jag missar helt? Är det rentav en allegori över Chiles kluvna situation. Vad gjorde den där Rodolfo egentligen som officer under Pinochet-tiden, måste man ju undra. Men om det är en sådan berättelse gömd under Glorias vingliga väg tycker jag det hade varit rimligt att ge oss icke-chilenska biobesökare lite fler ledtrådar.

Publicerat i film | Etiketter Gloria, Paulina Garcia | 8 kommentarer

Halvårskoll

Postat den 28 december, 2013 av Karin

Halvårskoll är dagen lördagstema. Jag bläddrar tillbaka och försöker hitta någon röd tråd. Det verkar mest vara blommor och blad som dominerar, så det får bli temat för halvåret som gick.

Stjärnflockan slår ut med armarna och utbrister ”Välkomna!” till alla som kom och hälsade på i Horndal i juli.

Andra lördagen i augusti firas Johan-Olovdagen vid Tvåbo. Någon läser en novell av Johan-Olov, några spelar och sjunger, någon berättar. Vi äter sme’mat och dricker kaffe med kringlor. Och på alla bord ska det finnas blommor. Mer om Johan-Olov-dagen här: http://johan-olov.se/?p=204

En lång varm och skön höst. Men krolliljorna visste när det var dags att sätta frö.

I oktober var det dags att hälsa på vänner i Israel och trots att jag nästan strök med, var det en väldigt positiv upplevelse. Mer om äventyret här: https://www.karinenglund.com/2013/10/allt-som-inte-dodar-dig-blir-ett-bra-blogginlagg/

I november var det dags att plocka in utemöbler, rusta för vintern, sätta in innanfönster, mm. Här en bild från bagarstugan i ett av husen med en kurbits som min mamma målade på 1960-talet.

I dag ser det ut så här vid vår stuga. Gräset är grönt och vi får ledigt från snöskottandet. Inga klagomål från mitt håll.

Här finns övriga lördagsbloggare: Gnuttan Helena Karin på Pettas Livsrummet musikanta Olgakatt, Pysseliten och i Januari tar HeLena över.

Trevlig avslutning på året önskas alla och ett bra 2014!

Publicerat i Att odla, Att resa, Lördagstema | Etiketter halvårskoll, lördagstema | 7 kommentarer

Årets julklapp

Postat den 27 december, 2013 av Karin

Det verkar vara många som fått samma julklappsbok i år och jag har själv gett bort den till höger och vänster: Lotta Lundgrens Tio lektioner i matlagning, men kanske allra mest om hur man gör när man lagar mat. Den är klok, kunnig och klarsynt. Samt lite lagom galen. Mången förälder ler igenkännande:

”Det finns många destruktiva krafter som vill beröva en människa hennes lust, motivation och förmåga att laga mat. Den mest kraftfulla är kort och gott BARN.”

Jodå, Lundgren försäkrar att hon tycker att det är barn, egna eller andras, som gör livet meningsfullt och att barn visserligen kommer till livet ”med uppdraget att stampa sönder ens lilla liv och göra konfetti av allt man trodde var viktigt, men det är ett rimligt pris med tanke på allt fint man får tillbaka.”

Men det kan ofta vara svårt att få dem att äta den mat vi väljer åt dem på det sätt som vi vuxna anser vara lämpligt.

Hon skildrar hur hon försökt allt, till exempel att servera middagen ”i dock- servisen, sittandes i badkaret med en rolig hatt på skallen”.

Hon har testat olika rätter ”inklusive pilgrimsmusslor, blodpudding, bräss, pekinganka, pizza, och Hummer Thermidor, vid alla tänkbara tidpunkter på dygnet. Inget av detta har fungerat. I alla fall inte över tid.” Räddningen heter fiskpinnar. Och att stålsätta sig mentalt:

”Negativa utlåtanden från matgäster som rutinmässigt äter sina egna snorkråkor är faktiskt inte något att bry sig om. Om det ändå blir knepigt att värja sig mot klagolåten, gör som alla moderna ledarskapsutbildade chefer nuförtiden: låt barnen prata på, tänk på annat och upprepa att ’jag hör vad du säger’.” Ett bra köttfärssåsrecept avslutar kapitlet.

På samma sätt går hon igenom matlagningens olika aspekter, med rubriker som Verktyg, Smak, Pengar och Instinkt. En mycket rolig och användbar bok om att laga och äta mat!

Publicerat i Böcker, Livet, vikten | Etiketter årets julklapp, Lotta Lundgren, Tio lektioner i matlagning | 8 kommentarer

Redaktörns julnötter

Postat den 25 december, 2013 av Karin

Så här års brukar redaktörn kapa bloggen för att bjuda på lite julnötter. Här är årets nöthög, som liknar högskoleprovet, lite ordkunskap, lite logik, lite naturkunskap. Nötterna finns också som pdf-fil, för er som vill skriva ut dem och klura vidare i lugn och ro.

De som har kommentarer, listiga ledtrådar som kan hjälpa andra på traven, som har kört fast och behöver hjälp eller som har frågor om frågorna kan använda kommentarsfältet. Facit kommer kring trettonhelgen. De som har knäckt nötterna kan skriva till nötansvarig redaktör: martin.lblm(at)gmail.com senast den 5 januari. Bokpriser utlovas. Lycka till!

I. Ordkunskap.

Homonymer kallas ord som stavas lika men har helt olika betydelser. Ett exempel är ordet bok, som dels kan betyda träd som växer i södra Sverige, dels de böcker som vi läser. Uppgiften är att gissa homonymerna nedan, alla substantiv. Några har två olika betydelser, andra tre. Nästan alla är vad jag kallar ”äkta” homonymer, dvs substantiven är inte uppenbart härledda från varandra. (En oäkta homonym är t ex substantivet ”slag”, som dels kan vara ett knytnävsslag och dels en militär drabbning, men båda orden har samma ursprung).

Alla homonymerna nedan går att hitta i Svenska Akademins ordlista. Som lite hjälp på traven kan jag säga att ingen av de tio homonymerna nedan innehåller mer än fyra bokstäver.

Exempel:

0.a Träd i södra Sverige (=BOK)
0.b Viktig förr i skolan (=BOK)

Hitta homonymerna:

1.a Viktigt för kockar
1.b Viktigt för fanatiker
1.c Viktigt för riksdagsledamöter

2.a Tänk 80
2.b Tänk 1988, 1991 och 1994
2.c Tänk stort

3.a Slakteriterm
3.b Finns i moderna kök

4.a Dröm för flicka
4.b Dröm för kossa

5.a Mardröm för vattenvarelse
5.b Önskade bisarr greve

6.a Beundrad för sin styrka
6.b Ofta mer värdefull än innehållet

7.a Inget för den köpmedvetne
7.b Tillåtet för män på fotbollsplan

8.a Ingår i lekamen
8.b Populärt i England
8.c Förvillar spårhundar

9.a Gillar militärer
9.b Finns i fjällen
9.c Motoriskt oumbärlig

10.a Kan man räkna med
10.b Ingick i skolgymnastik
10.c Också en hierarki
10.d Flugig förbindelselänk
10.e För blytunga typer

II. Ren och skär logik – och konsten att avslöja lögner

1. En pojke och en flicka bekantar sig med varandra.
– Jag är en pojke, säger barnet med mörkt hår.
– Jag är en flicka, säger barnet med blont hår.
Åtminstone ett av barnen ljuger.
Fråga: Vilken färg på håret har pojken och vilken färg på håret har flickan?
(Som det heter på högskoleprovet: tillräcklig information för att besvara frågan finns i lämnade faktauppgifter)

Du plockar först ur en slumpmässigt vald påse ut en ädelsten och den visar sig vara röd.
Ur vilken påse ska du plocka ut nästa ädelsten för att med största sannolikhet maximalt öka din rikedom? Eller spelar det ingen roll för din chans till maximal rikedom ur vilken påse du drar din nästa sten? (OBS! På denna fråga finns bara ett korrekt svar)

Kalle Kulor: ”Jag är oskyldig”.
Girige Herbert: ”Jag är oskyldig”.
Förslagne Doris: ”Girige Herbert är den skyldige”.
”Tack för de svaren”, säger utredaren och ber sina polisassistenter arrestera en av de misstänkta direktörerna som skyldig till svindeln. Och du vet väl också vem som är skurken i detta drama?

Och om du tänker efter noga kommer du nog på den enda möjliga frågan.

5. A och B är två siffror mellan 0–9, inte nödvändigtvis olika. De två logiskt begåvade syskonen Karin och Gunnar försöker klura ut vilka siffrorna är. Karin känner till siffrornas summa och Gunnar känner till siffrornas produkt.
Följande samtal äger rum:
Karin: ”Jag vet inte vilka siffrorna är.”
Gunnar: ”Inte jag heller, men jag visste att du inte kunde veta det.”
Karin: ”Vad bra, nu vet jag vilka de två siffrorna är!”
Gunnar: ”Jag med!”

Vilka är de två siffrorna? (Jag lovar. Tillräcklig information finns ovan för att lösa problemet. Mattekunskaper på mellanstadienivå behövs dock).

III. Optiska villor, andra villor och lite fysik

Varje julnötstävling bör innehålla ett tändsticksproblem. I uppställningen nedan är uppgiften att flytta en enda sticka så du får en korrekt ekvation (åtminstone om du nöjer dig med två decimaler).