Så här års brukar redaktörn kapa bloggen för att bjuda på lite julnötter. Här är årets nöthög, som liknar högskoleprovet, lite ordkunskap, lite logik, lite naturkunskap. Nötterna finns också som pdf-fil, för er som vill skriva ut dem och klura vidare i lugn och ro.
De som har kommentarer, listiga ledtrådar som kan hjälpa andra på traven, som har kört fast och behöver hjälp eller som har frågor om frågorna kan använda kommentarsfältet. Facit kommer kring trettonhelgen. De som har knäckt nötterna kan skriva till nötansvarig redaktör: martin.lblm(at)gmail.com senast den 5 januari. Bokpriser utlovas. Lycka till!
I. Ordkunskap.
Homonymer kallas ord som stavas lika men har helt olika betydelser. Ett exempel är ordet bok, som dels kan betyda träd som växer i södra Sverige, dels de böcker som vi läser. Uppgiften är att gissa homonymerna nedan, alla substantiv. Några har två olika betydelser, andra tre. Nästan alla är vad jag kallar ”äkta” homonymer, dvs substantiven är inte uppenbart härledda från varandra. (En oäkta homonym är t ex substantivet ”slag”, som dels kan vara ett knytnävsslag och dels en militär drabbning, men båda orden har samma ursprung).
Alla homonymerna nedan går att hitta i Svenska Akademins ordlista. Som lite hjälp på traven kan jag säga att ingen av de tio homonymerna nedan innehåller mer än fyra bokstäver.
Exempel:
0.a Träd i södra Sverige (=BOK)
0.b Viktig förr i skolan (=BOK)
Hitta homonymerna:
1.a Viktigt för kockar
1.b Viktigt för fanatiker
1.c Viktigt för riksdagsledamöter
2.a Tänk 80
2.b Tänk 1988, 1991 och 1994
2.c Tänk stort
3.a Slakteriterm
3.b Finns i moderna kök
4.a Dröm för flicka
4.b Dröm för kossa
5.a Mardröm för vattenvarelse
5.b Önskade bisarr greve
6.a Beundrad för sin styrka
6.b Ofta mer värdefull än innehållet
7.a Inget för den köpmedvetne
7.b Tillåtet för män på fotbollsplan
8.a Ingår i lekamen
8.b Populärt i England
8.c Förvillar spårhundar
9.a Gillar militärer
9.b Finns i fjällen
9.c Motoriskt oumbärlig
10.a Kan man räkna med
10.b Ingick i skolgymnastik
10.c Också en hierarki
10.d Flugig förbindelselänk
10.e För blytunga typer
II. Ren och skär logik – och konsten att avslöja lögner
1. En pojke och en flicka bekantar sig med varandra.
– Jag är en pojke, säger barnet med mörkt hår.
– Jag är en flicka, säger barnet med blont hår.
Åtminstone ett av barnen ljuger.
Fråga: Vilken färg på håret har pojken och vilken färg på håret har flickan?
(Som det heter på högskoleprovet: tillräcklig information för att besvara frågan finns i lämnade faktauppgifter)
2. Du har framför dig tre tygpåsar om vilka du vet att var och en innehåller två ädelstenar. I en påse är båda ädelstenarna röda, i en påse är båda gröna och i en påse är en ädelsten röd och en ädelsten grön. Du vet att de röda ädelstenarna är 100 gånger mer värdefulla än de gröna. Du får ta två ädelstenar ur påsarna och behålla dem. Men hur ska du gå tillväga?
Du plockar först ur en slumpmässigt vald påse ut en ädelsten och den visar sig vara röd.
Ur vilken påse ska du plocka ut nästa ädelsten för att med största sannolikhet maximalt öka din rikedom? Eller spelar det ingen roll för din chans till maximal rikedom ur vilken påse du drar din nästa sten? (OBS! På denna fråga finns bara ett korrekt svar)
3. Statens finansinspektion har upptäckt en olaglig spekulation mot den svenska kronan. En undersökning visar att en av tre storbanksdirektörer måste vara skyldig. Av utredningen framgår att bara en av dem kan tala sanning, medan de två andra två måste ljuga konsekvent av olika skäl. På utredarens direkta fråga om vem som har svindlat den svenska staten får han följande svar:
Kalle Kulor: ”Jag är oskyldig”.
Girige Herbert: ”Jag är oskyldig”.
Förslagne Doris: ”Girige Herbert är den skyldige”.
”Tack för de svaren”, säger utredaren och ber sina polisassistenter arrestera en av de misstänkta direktörerna som skyldig till svindeln. Och du vet väl också vem som är skurken i detta drama?
4. Du har just levt klart och befinner dig nu i Sankte Pers väntrum för att slussas vidare till antingen Paradiset eller Helvetet. Men Paradiset håller på att bli överbefolkat så Sankte Per har föranstaltat en liten test för applikanterna.
I väntrummet som du förts in i finns bara två utgångar varav den ena leder till Paradiset och den andra till Helvetet. Men du vet inte vilken utgång som leder vart. Varje utgång vaktas av en dörrvakt varav den ena konsekvent ljuger och den andra konsekvent talar sanning. Men du vet inte vilken. Du har därmed ingen aning om det är lögnaren som vaktar dörren till Paradiset eller om det är sannıngssägaren.
Sankte Per säger att du får bara ställa en enda fråga som kan besvaras med enbart ja eller nej till en av dörrvakterna för att ta reda på dörren till Paradiset. Han påpekar att de båda dörrvakterna är införstådda med valsituationens villkor. Du svarar gnälligt att uppgiften är omöjlig att lösa eftersom du varken vet vilken av dörrvakterna som ljuger eller vart dörrarna går. Sankte Per skrattar gott och säger att en enda fråga räcker, men vem har sagt att det ska vara lätt att komma till Paradiset.
Och om du tänker efter noga kommer du nog på den enda möjliga frågan.
5. A och B är två siffror mellan 0–9, inte nödvändigtvis olika. De två logiskt begåvade syskonen Karin och Gunnar försöker klura ut vilka siffrorna är. Karin känner till siffrornas summa och Gunnar känner till siffrornas produkt.
Följande samtal äger rum:
Karin: ”Jag vet inte vilka siffrorna är.”
Gunnar: ”Inte jag heller, men jag visste att du inte kunde veta det.”
Karin: ”Vad bra, nu vet jag vilka de två siffrorna är!”
Gunnar: ”Jag med!”
Vilka är de två siffrorna? (Jag lovar. Tillräcklig information finns ovan för att lösa problemet. Mattekunskaper på mellanstadienivå behövs dock).
III. Optiska villor, andra villor och lite fysik
Varje julnötstävling bör innehålla ett tändsticksproblem. I uppställningen nedan är uppgiften att flytta en enda sticka så du får en korrekt ekvation (åtminstone om du nöjer dig med två decimaler).

Vilken sticka vill du flytta och varthän?
2. Två pojkar vill ta sig över en å. Båda pojkarna är dåliga simmare och skulle drunkna om de försökte ta sig simmande över ån. Enda sättet att ta sig över är därför att använda en liten båt, som bara kan ta en person åt gången. Båten kan inte återvända på egen hand och den dras inte med rep eller andra anordningar, ändå lyckas de båda pojkarna ta sig över ån. Hur förklarar du det?
3. En gurka består till 99% av vatten. Efter att ha legat i solen på ett bord ett längre tag består den bara till 98% av vatten. Hur mycket väger gurkan nu om den från början vägde ett kilo?
4. Erik kör sin motorcykel ett varv (= 1 km) på en motorbana i 30 km/t. Han ska köra ett varv till och vill efter det varvet ha kört de båda varven med en medelhastighet av 60 km/t. Hur fort måste han köra det andra varvet för att teoretiskt klara av uppgiften? (OBS. Svaret är INTE 90 km/t).
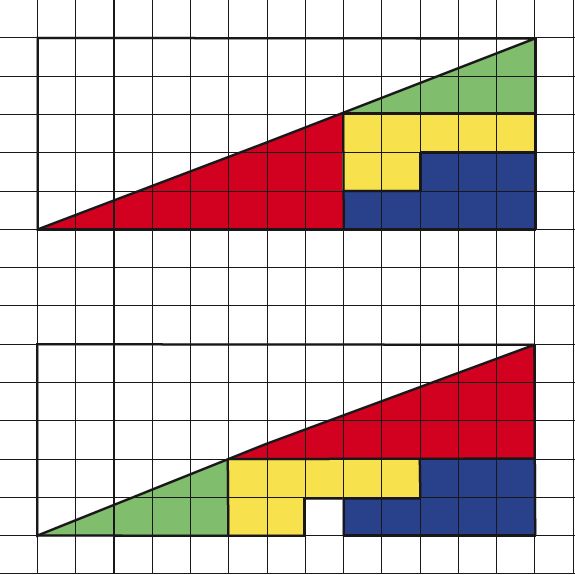
5. Betrakta de två trianglarna nedan. De är byggda av samma färgglada bitar, men i den nedre triangeln har smugit sig in en vit kvadrat. Kan du förklara hur den har uppstått?
SLUT!

























