 Häromkvällen diskuterades skola, så där som man alltid gör när man ses, några stycken. Efteråt kom jag att tänka på en matematikhistoria, som borde kunna få en fortsättning.
Häromkvällen diskuterades skola, så där som man alltid gör när man ses, några stycken. Efteråt kom jag att tänka på en matematikhistoria, som borde kunna få en fortsättning.
Och så sökte jag på nätet efter en lämplig illustration, gärna ett ex av matteböcrna i serien ”Hej matematik”, men det gick inte att hitta, bara en liten ruta med själva loggan.
Men så kom Lotten till undsättning med ett helt inlägg om matteundervisningen (mycket läs- och tänkvärt!) och därifrån har jag plockat girafferna.
Men i alla fall, den där mattehistorien. Jag tror den kom till när uppgivenheten bland lärarna var som störst efter införandet och avskaffandet av mängdläran under 70- och 80-talet:
1950 — En bonde säljer en säck potatis för 20 kr. Framställningskostnaderna är 4/5 av priset. Hur stor är vinsten uttryckt i kronor?
Många elever hade dock svårt för bråkräkning så uppgiften modifierades och flyttades till årskurs 7.
1960 — En bonde säljer en säck potatis för 20 kr. Framställningskostnaderna är 16 kr. Var snäll och räkna ut vinsten.
I början av 1970-talet infördes mängdläran och uppgiften flyttades årskurs 9.
1970 — En bonde säljer en mängd potatis (A) för en mängd pengar (B). B är mängden av alla delar BE för vilka gäller; BE är en krona. I streckmängdform måste du för mängden B göra tjugo små streck [/ / / / / / / / / / / / / / / / / / / /], ett för varje krona. Mängden av framställnings- kostnaderna (C) är sexton små streck [/ / / / / / / / / / / / / / / /]. Rita bilden av mängden C som en delmängd av mängden B och angiv resultatmängden (D), som ger svaret på frågan: Vad är kardinaltalet för vinstmängden?
Det blev för krångligt, så kring 1980 övergavs mängdläran. Uppgiften omformulerades och flyttades till årskurs 1 på gymnasiet.
1980 — En bonde säljer en säck potatis för 20 kr. Framställningskostnaderna är 4/5 därav, vilket är 16 kr. Vinsten uppgår till 1/5, vilket är lika med 4 kr. Stryk under ordet ”potatis” och diskutera för- och nackdelar med potatisodling med din bänkkamrat.
”Jag tycker detta är ett utmärkt bevis på en riktig utveckling”, påpekar Skolverkets expert på matematikens pedagogik, Pia Get. ”Vid en undersökning fann vi att många elever på gymnasiet klarade 1980 års uppgift, både att stryka under rätt ord och att klara den psykosociala samvaron med sina kamrater. Uppgiften är dock i svåraste laget för en del elever, och vi funderar på att i en kommande version redan i uppgiftens text stryka under ordet ’potatis’, vilket kommer att ge eleverna mer tid för stimulerande kamratsamtal.”
Som ni ser saknas det exempel för 90-talet och 00-talet.
Och apropå räkna, så har den tredje fiskgjuseungen kläckts, lilla Estrid, men hon är svår att få syn på. Så här såg det ut hemma hos fiskgjusarna för en stund sedan. Man ser Estrids äggskal och man ser rumpan på henne, mellan syskonen Estelle och Estellan.

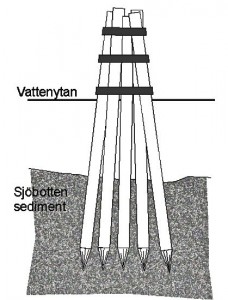 Och när vi ändå är inne på sjötermer kan jag tipsa om uppdykande dykdalber, som man kan läsa om hos Livsrummet.
Och när vi ändå är inne på sjötermer kan jag tipsa om uppdykande dykdalber, som man kan läsa om hos Livsrummet.



























